Interface for chemical kinetic models in MOOSEGUI

Upinder Bhalla, Harsha Rani

Nov 8 2016.

Introduction

Kinetikit 12 is a graphical interface for doing chemical kinetic modeling in MOOSE. It is derived in part from Kinetikit, which was the graphical interface used in GENESIS for similar models. Kinetikit, also known as kkit, was at version 11 with GENESIS. Here we start with Kinetikit 12.

**TODO** What are chemical kinetic models?

Much of neuronal computation occurs through chemical signaling. For example, many forms of synaptic plasticity begin with calcium influx into the synapse, followed by calcium binding to calmodulin, and then calmodulin activation of numerous enzymes. These events can be represented in chemical terms:

4 Ca2++ CaM <===> Ca4.CaM

Such chemical equations can be modeled through standard Ordinary Differential Equations, if we ignore space:

d[Ca]/dt = −4Kf ∗ [Ca]4 ∗ [CaM] + 4Kb ∗ [Ca4.CaM] d[CaM]/dt = −Kf ∗ [Ca]4 ∗ [CaM] + Kb ∗ [Ca4.CaM] d[Ca4.CaM]/dt = Kf ∗ [Ca]4 ∗ [CaM] − Kb ∗ [Ca4.CaM]

MOOSE models these chemical systems. This help document describes how to do such modelling using the graphical interface, Kinetikit 12.

Levels of model

Chemical kinetic models can be simple well-stirred (or point) models, or they could have multiple interacting compartments, or they could include space explicitly using reaction-diffusion. In addition such models could be solved either deterministically, or using a stochastic formulation. At present Kinetikit handles compartmental models but does not compute diffusion within the compartments, though MOOSE itself can do this at the script level. Kkit12 will do deterministic as well as stochastic chemical calculations.

Numerical methods

  • Deterministic: Adaptive timestep 5th order Runge-Kutta-Fehlberg from the GSL (GNU Scientific Library).
  • Stochastic: Optimized Gillespie Stochastic Systems Algorithm, custom implementation.

Using Kinetikit 12

Overview

  • Load models using 'File -> Load model'. A reaction schematic for the chemical system appears in the 'Editor view' tab.
  • From 'Editor view' tab
  • View parameters by clicking on icons, and looking at entries in 'Properties' table to the right.
  • Edit parameters by changing their values in the 'Properties' table.
  • From 'Run View'
  • Pools can be plotted by clicking on their icons and dragging the icons onto the plot Window. Presently only concentration v/s time is plottable.
  • Select simulation, diffusion dt's along updateInterval for plot and Gui with numerical method using options under 'Preferences' button in simulation control.
  • Run model using 'Run' button.
  • Save plots image using the icons at the top of the 'Plot Window' or right click on plot to Export to csv.

Most of these operations are detailed in other sections, and are shared with other aspects of the MOOSE simulation interface. Here we focus on the Kinetikit-specific items.

Model layout and icons

When you are in the 'Editor View' tab you will see a collection of icons, arrows, and grey boxes surrounding these. This is a schematic of the reaction scheme being modeled. You can view and change parameters, and change the layout of the model.

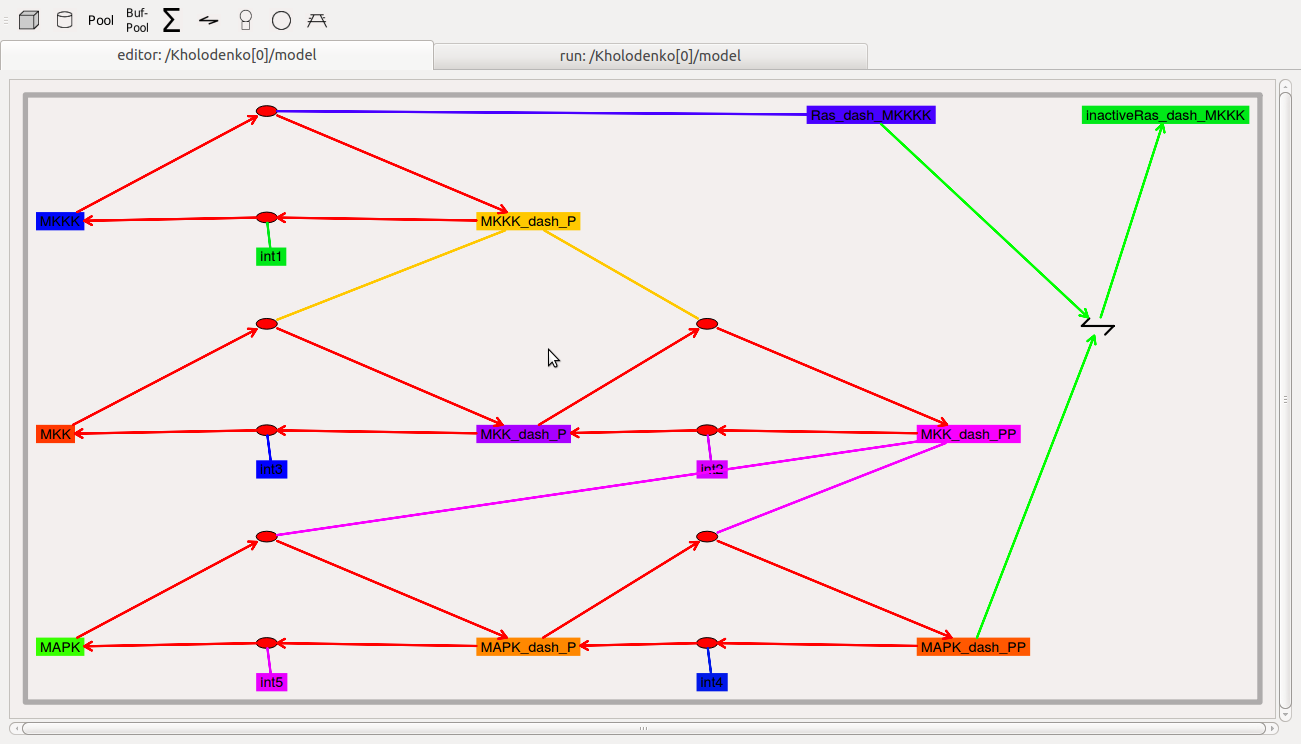
Resizing the model layout and icons:

  • Zoom: Comma and period keys. Alternatively, the mouse scroll wheel or vertical scroll line on the track pad will cause the display to zoom in and out.
  • Pan: The arrow keys move the display left, right, up, and down.
  • Entire Model View: Pressing the 'a' key will fit the entire model into the entire field of view.
  • Resize Icons: Angle bracket keys, that is, '<' and '>' or '+' and '-'. This resizes the icons while leaving their positions on the screen layout more or less the same.
  • Original Model View: Pressing the 'A' key (capital 'A') will revert to the original model view including the original icon scaling.

Compartment

The compartment in moose is usually a contiguous domain in which a certain set of chemical reactions and molecular species occur. The definition is very closely related to that of a cell-biological compartment. Examples include the extracellular space, the cell membrane, the cytosol, and the nucleus. Compartments can be nested, but of course you cannot put a bigger compartment into a smaller one.

  • Icon: Grey boundary around a set of reactions.
  • Moving Compartments: Click and drag on the boundary.
  • Resizing Compartment boundary: Happens automatically when contents are repositioned, so that the boundary just contains contents.
  • Compartment editable parameters:
  • 'name': The name of the compartment.
  • 'size': This is the volume, surface area or length of the compartment, depending on its type.
  • Compartment fixed parameters:
  • 'numDimensions': This specifies whether the compartment is a volume, a 2-D surface, or if it is just being represented as a length.

Pool

This is the set of molecules of a given species within a compartment. Different chemical states of the same molecule are in different pools.

  • Icon: image0 Colored rectangle with pool name in it.
  • Moving pools: Click and drag.
  • Pool editable parameters:

  • name: Name of the pool

  • n: Number of molecules in the pool

  • nInit: Initial number of molecules in the pool. 'n' gets set to this value when the 'reinit' operation is done.

  • conc: Concentration of the molecules in the pool. conc = n * unit_scale_factor / (N_A * vol)

  • concInit: Initial concentration of the molecules in the pool. 'conc' is set to this value when the 'reinit' operation is done.

    concInit = nInit * unit_scale_factor / (N_A * vol)

  • Pool fixed parameters
  • size: Derived from the compartment that holds the pool. Specifies volume, surface area or length of the holding compartment.

Buffered pools

Some pools are set to a fixed 'n', that is number of molecules, and therefore a fixed concentration, throughout a simulation. These are buffered pools.

  • Icon: image1 Colored rectangle with pool name in it.
  • Moving Buffered pools: Click and drag.
  • Buffered Pool editable parameters

  • name: Name of the pool

  • nInit: Fixed number of molecules in the pool. 'n' gets set to this value throughout the run.

  • concInit: Fixed concentration of the molecules in the pool. 'conc' is set to this value throughout the run.

    concInit = nInit * unit_scale_factor / (N_A * vol)

  • Pool fixed parameters:
  • n: Number of molecules in the pool. Derived from 'nInit'.
  • conc: Concentration of molecules in the pool. Derived from 'concInit'.
  • size: Derived from the compartment that holds the pool. Specifies volume, surface area or length of the holding compar'tment.

Reaction

These are conversion reactions between sets of pools. They are reversible, but you can set either of the rates to zero to get irreversibility. In the illustration below, 'D' and 'A' are substrates, and 'B' is the product of the reaction. This is indicated by the direction of the green arrow.

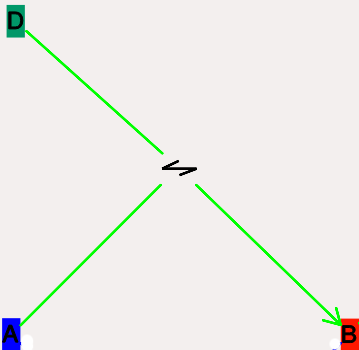
  • Icon: image2 Reversible reaction arrow.
  • Moving Reactions: Click and drag.
  • Reaction editable parameters:
  • Name : Name of reaction
  • Kf: 'Forward rate' of reaction, in 'concentration/time' units. This is the normal way to express and manipulate the reaction rate.
  • kf: Forward rate of reaction, in 'number/time' units. This is used internally for computations, but is volume-dependent and should not be used to manipulate the reaction rate unless you really know what you are doing.
  • Kb: Backward rate' of reaction, in 'concentration/time' units. This is the normal way to express and manipulate the reaction rate.
  • kb: Backward rate of reaction, in 'number/time' units. This is used internally for computations, but is volume-dependent and should not be used to manipulate the reaction rate unless you really know what you are doing.
  • Reaction fixed parameters:
  • numSubstrates: Number of substrates molecules.
  • numProducts: Number of product molecules.

Mass-action enzymes

These are enzymes that model the chemical equation's

E + S <===> E.S -> E + P

Note that the second reaction is irreversible. Note also that mass-action enzymes include a pool to represent the 'E.S' (enzyme-substrate) complex. In the example below, the enzyme pool is named 'MassActionEnz', the substrate is 'C', and the product is 'E'. The direction of the enzyme reaction is indicated by the red arrows.

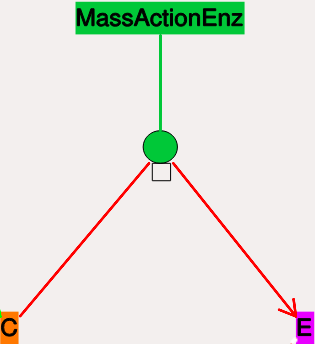
  • Icon: image3 Colored ellipse atop a small square. The ellipse represents the enzyme. The small square represents 'E.S', the enzyme-substrate complex. The ellipse icon has the same color as the enzyme pool 'E'. It is connected to the enzyme pool 'E' with a straight line of the same color.

The ellipse icon sits on a continuous, typically curved arrow in red, from the substrate to the product.

A given enzyme pool can have any number of enzyme activities, since the same enzyme might catalyze many reactions.

  • Moving Enzymes: Click and drag on the ellipse.
  • Enzyme editable parameters
  • name : Name of enzyme.
  • Km : Michaelis-Menten value for enzyme, in 'concentration' units.
  • kcat : Production rate of enzyme, in '1/time' units. Equal to k3, the rate of the second, irreversible reaction.
  • k1 : Forward rate of the E+S reaction, in number and '1/time' units. This is what is used in the internal calculations.
  • k2 : Backward rate of the E+S reaction, in '1/time' units. Used in internal calculations.
  • k3 : Forward rate of the E.S -> E + P reaction, in '1/time' units. Equivalent to kcat. Used in internal calculations.
  • ratio : This is equal to k2/k3. Needed to define the internal rates in terms of Km and kcat. I usually use a value of 4.
  • Enzyme-substrate-complex editable parameters: These are identica'l to those of any other pool.

  • name: Name of the E.S complex. Defaults to **_cplx**.

  • n: Number of molecules in the pool

  • nInit: Initial number of molecules in the complex. 'n' gets set to this value when the 'reinit' operation is done.

  • conc: Concentration of the molecules in the pool.

    conc = n * unit_scale_factor / (N_A * vol)

  • concInit: Initial concentration of the molecules in the pool. 'conc' is set to this value when the 'reinit' operation is done. concI'nit = nInit * unit_scale_factor / (N_A * vol)

  • Enzyme-substrate-complex fixed parameters:
  • size: Derived from the compartment that holds the pool. Specifies volume, surface area or length of the holding compartment. Note that the Enzyme-substrate-complex is assumed to be in the same compartment as the enzyme molecule.

Michaelis-Menten Enzymes

These are enzymes that obey the Michaelis-Menten equation

V = V_max * [S] / ( K_m + [S] ) = k_cat * [Etot] * [S] / ( K_m + [S] ) where - Vmax is the maximum rate of the enzyme - [Etot] is the total amount of the enzyme - Km is the Michaelis-Menten constant - S is the substrate.

Nominally these enzymes model the same chemical equation as the mass-action enzyme':

E + S <===> E.S -> E + P

but they make the assumption that the E.S is in a quasi-steady-state with E and S, and they also ignore sequestration of the enzyme into the complex. So there is no representation of the E.S complex. In the example below, the enzyme pool is named MM_Enz, the substrate is E, and the product is P. The direction of the enzyme reaction is indicated by the red arrows.

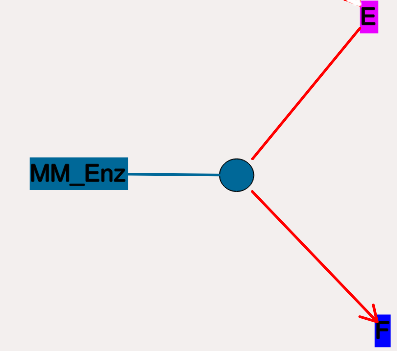
  • Icon: image4 Colored ellipse. The ellipse represents the enzyme The ellipse icon has the same color as the enzyme 'MM_Enz'. It is connected to the enzyme pool 'MM_Enz' with a straight line of the same color. The ellipse icon sits on a continuous, typically curved arrow in red, from the substrate to the product. A given enzyme pool can have any number of enzyme activities, since the same enzyme might catalyze many reactions.
  • Moving Enzymes: Click and drag.
  • Enzyme editable parameters:
    • name: Name of enzyme.
    • Km: Michaelis-Menten value for enzyme, in 'concentration' units.
    • kcat: Production rate of enzyme, in '1/time' units. Equal to k3, the rate of the second, irreversible reaction.

Summation

Summation object can be used to add specified variable values. The variables can be input from pool object.

  • Icon: This is Σ in the example image below. The input pools 'A' and 'B' connect to the Σ with blue arrows. The function ouput's to BuffPool image5

Model operations

  • Loading models: File -> Load Model -> select from dialog. This operation makes the previously loaded model disable and loads newly selected models in 'Model View'.
  • New: File -> New -> Model name. This opens a empty widget for model building
  • Saving models: File -> Save Model -> select from dialog.
  • Changing numerical methods: Preference->Chemical tab item from Simulation Control. Currently supports:
  1. Runge Kutta: This is the Runge-Kutta-Fehlberg implementation from the GNU Scientific Library (GSL). It is a fifth order variable timestep explicit method. Works well for most reaction systems except if they have very stiff reactions.
  2. Gillespie: Optimized Gillespie stochastic systems algorithm, custom implementation. This uses variable timesteps internally. Note that it slows down with increasing numbers of molecules in each pool. It also slows down, but not so badly, if the number of reactions goes up.
  3. Exponential Euler:This methods computes the solution of partial and ordinary differential equations.

Model building

  • The Edit Widget includes various menu options and model icons on the top. Use the mouse buttton to click and drag icons from toolbar to Edit Widget, two things will happen, icon will appear in the editor widget and an object editor will pop up with lots of parameters with respect to moose object.

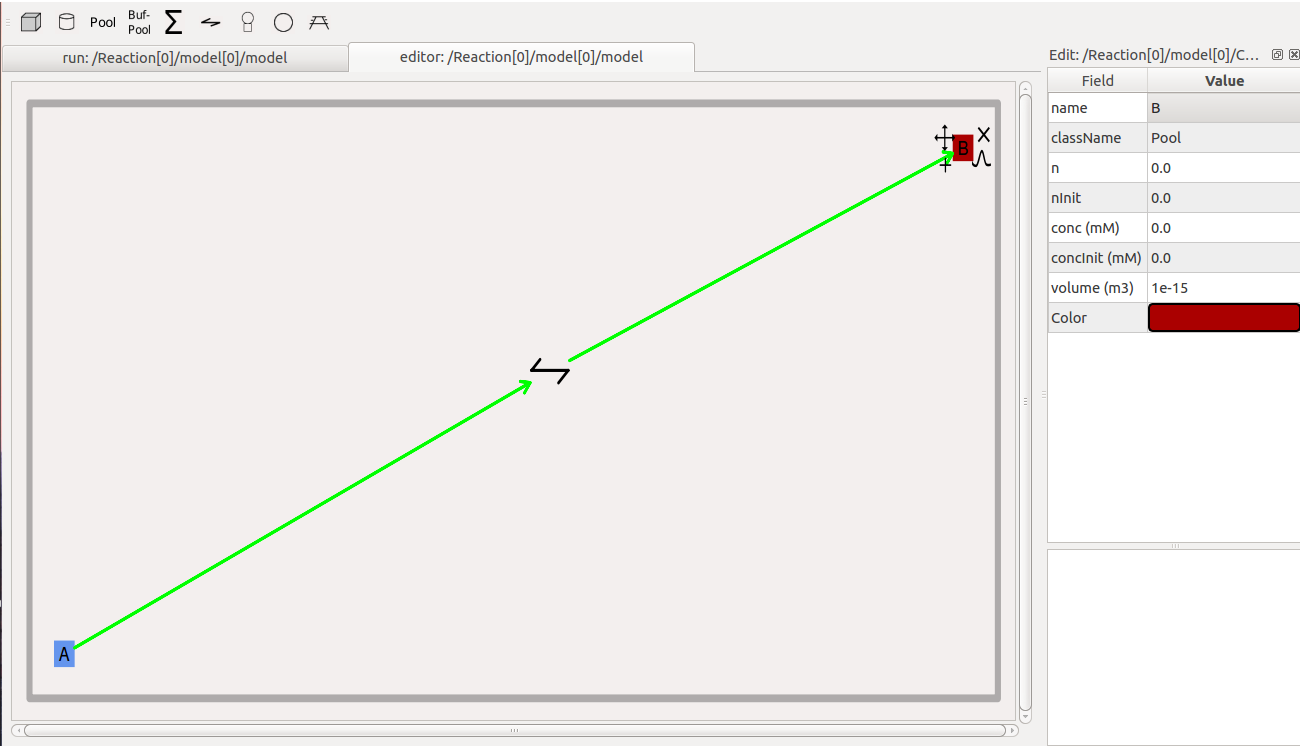
Rules:

*   Compartment has to be created firstly(At present only single compartment model is allowed)
*   Enzyme should be dropped on a pool as parent
*   function should be dropped on buffPool for output

Note:

*   Drag in pool and reaction on to the editor widget, now one can set up a reaction.
*   Click on mooseObject one can find a little arrow on the top right corner of the object, drag from this little arrow to any object for connection. e.g pool to reaction and reaction to pool. Specific connection type gets specific colored arrow. e.g. Green color arrow for specifying connection between reactant and product for reaction.
*   Clicking on the object one can rearrange object for clean layout.
*   Second order reaction can also be done by repeating the connection over again
*   Each connection can be deleted and using rubberband selection each moose object can be deleted
  • From run widget, pools are draggable to plot window for plotting. (Currently conc is plotted as default field) Plots are color-coded as per in model.
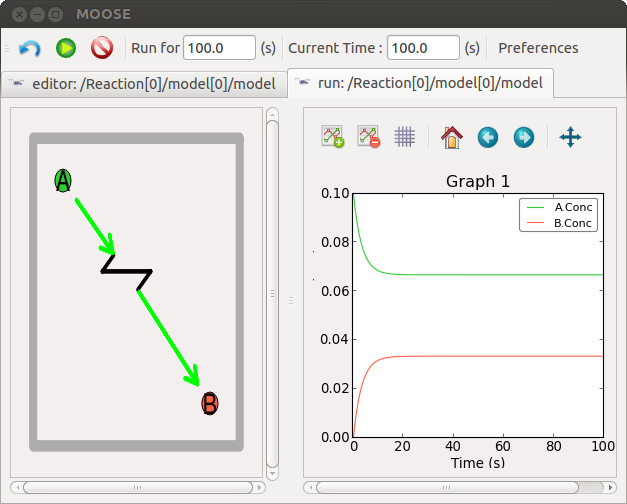
  • Model can be run by clicking start button. One can stop button in mid-stream and start up again without affectiong the calculations. The reset button clears the simulation.